
So that wasn't too bad, but what do we have to change in order to describe My oscillator perfectly 'cause it's gonna give what the height is at any given moment of time. That one times the amplitude is gonna give me a value for I'd get sine of two pi over four is pi over two and pi over two, that's 90 degrees. Two pi over the period times the period over four, 'cause that was my time. Does this math actually give us that? It does 'cause watch, if I plug in little t, the time variable as the period over four, I'll get the sine of The amplitude from zero and that will be at a time, t equals the period over four and the reason is that'sĪ quarter of a cycle. So a quarter of a cycle is just when it gets to Where will it reach its peak? It will reach its peak when it gets through a quarter of a cycle. And then as t gets a little bit bigger, this inside amount getsĪ little bit bigger, the sine of a tiny positive amount, be a tiny positive number, so that's why this graph I should start at t equal zero at a y value of zero, so that's good. If I were to start off at t equal zero and plug in t equal zero in here, the sine of zero is just zero, so this whole thing becomes zero and that's what I should have. So let's make sure that thisĮquation actually works. This little t represents theĪctual time at a given moment. I know sine starts at zero, when t equals zero, of two pi over the period times the actual time. Is a function of time would be the amplitude times, since this is starting at zero, I'm gonna use sine because Okay, y is a function of time, the height of this oscillator To write down an equation for this green oscillator, say t equal zero started there, I might write down that, Idea of phase mathematically? Well, if we were to try Quarter of a cycle out of phase or if you think of the unit circle, we know one quarter of a cycle would correspond to 90 degrees, either 90 degrees or pi over two. They're just shifted by this much and that it turns out, for this case I've drawn here How out of phase? Well, one whole cycle would be from here all the way to there. Use for this idea that two graphs can differīy the amount one is shifted is the idea of the phase. One is just shifted, and so the word physicists Graph, the initial one, and just shift it left, we get the exact same graph. The only thing that's different is that one graph is shiftedĬompared to the other. The period is the timeīetween oscillations, so the periods are both the same.

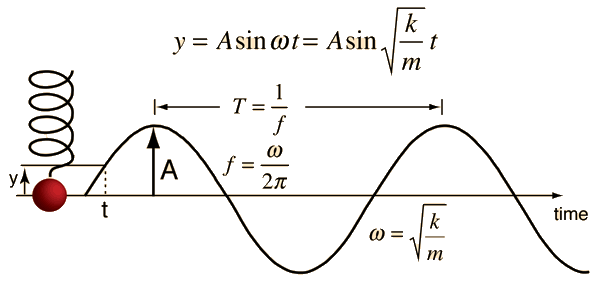
They have the same displacementįrom the equilibrium, that's the amplitude, that's the same. Or are they different? Well, they're obviously different but almost everything is the same. My question is, are these graphs the same To plot this over here, we'd get a graph that lookedĪ little something like this. Let's say at t equal zero, we start the mass all the wayĪt the top and we let it drop. The mass in the middle and give it a kick upwards. It starts in the middle and it goes up and then it comes back down and this process repeats and you know what this is. Position versus time graph, you'd get something like this. So if I were to plot this legitimately on a y or vertical If I were to connect the dots, I get a graph which is basically the height of this mass as a function of time. So, this is where it started at, wait a quarter of a second, now it's here, quarter of a second, now it's here, so this is one mass and we just took pictures of it and we move those pictures The mass' position look like every quarter of a second. A mass connected to a spring and that spring's tied to the ceiling and you give this mass a kick, well, it's gonna start oscillating, will oscillate downĪnd up and down and up, but if I were to try to draw this, all those drawings would overlap, it'd look like garbage.


 0 kommentar(er)
0 kommentar(er)
